In the annals of global mathematics, the name Choi Seok-jeong (Choi Seokjeong; 개명: 최석정, 1646–1715) deserves far more recognition. This brilliant polymath of the Joseon Dynasty was not only a high-ranking official and a political reformer during the reign of King Sukjong, but also one of the world’s earliest pioneers in advanced mathematical structures, most notably magic squares.
Who Was Choi Seok-jeong?

Choi Seok-jeong was a distinguished scholar, politician, and mathematician in late Joseon Korea. Though originally a member of the Westerners (Seo-in) political faction, he bravely opposed a fabricated treason case and aligned with the more moderate Southerners (So-ron). Beyond politics, Choi devoted his life to scholarly pursuits, with a profound focus on mathematics, astronomy, and philosophy.
His work exemplified the philosophy of “silhak” (실학) — practical learning rooted in empirical research and rational analysis. Among his greatest achievements was the systematic study of higher-dimensional magic squares, preceding the renowned work of Leonhard Euler(1707~1783) by decades.
What Is a Magic Square?
A magic square is a grid of numbers arranged so that the sum of each row, column, and diagonal is equal. For example, in a 3×3 magic square, all rows, columns, and diagonals sum to 15. Magic squares have historically held cultural, mathematical, and mystical significance across both Eastern and Western traditions.
In Joseon Korea, knowledge of magic squares was introduced through classical Chinese texts such as gujangsansul (九章算術, Nine Chapters on the Mathematical Art). Choi Seok-jeong went far beyond these roots, delving into multidimensional structures and developing his own rigorous mathematical frameworks.
Choi Seok-jeong’s Groundbreaking Work on Magic Squares
Higher-Dimensional Magic Squares
Unlike earlier works limited to 2D arrays, Choi explored 3D and even 4D magic squares, crafting systematic methods to construct them using mathematical principles and logic. He did not merely create arrangements by trial and error, but formalized generation algorithms, offering clarity on the structural rules that govern such squares.
Gusuryak (구수략, “A Brief Survey of Nine Numbers”)

Choi Seok-jeong’s pioneering 9th-order orthogonal Latin squares, the first in the world
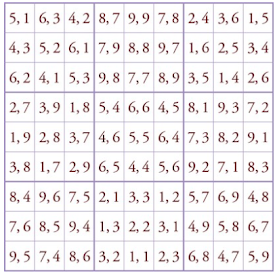
Image Explanation
Choi Seok-jeong’s 9th-order orthogonal Latin squares are expressed as nine 3×3 magic squares within a 9×9 square. A unique feature of this magic square is that not only do the sums of all rows, columns, and diagonals in the entire grid match, but the same holds true for each individual 3×3 magic square as well.
Choi Seok-jeong’s mathematical treatise Gusuryak contains a trove of advanced magic square constructions and theories. This includes the world’s first documented 9×9 orthogonal Latin square, a feat unmatched for decades even in Europe. Notably, Euler, in the 1740s, proved the existence of Latin squares, but did not produce such a complex 9×9 orthogonal version until much later.
Choi’s version was mathematically elegant and algorithmically constructed. Each of the 9 sub-3×3 squares within the full 9×9 matrix forms a magic square, and the overall 9×9 grid maintains the same magic constant across all rows, columns, and diagonals.
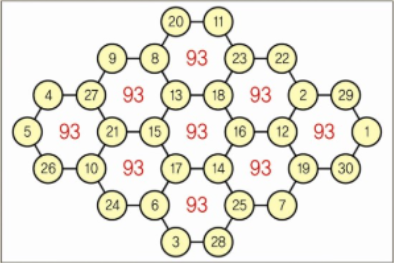
The Geometric Wonder of “Jisugwimundo”


Another of Choi’s inventions, the Jisugwimundo (지수귀문도), is a hexagonal magic diagram in which every radial axis of six cells sums to 93. This geometric symmetry reveals his deep understanding of both numerics and spatial design, blending mathematical beauty with philosophical symmetry.
Why Choi Seok-jeong’s Work Matters Today
Global Historical Significance
Choi Seok-jeong is the first known mathematician in the world to systematically study higher-dimensional and orthogonal Latin magic squares. His discoveries were made at least 67 years before Euler’s famous Latin square theory became known in the West.
A Foundation for Modern Fields
Choi’s insights laid conceptual foundations for several modern disciplines:
- Combinatorics & Design Theory: His orthogonal Latin square has been referenced in modern design theory, including the 2007 edition of Handbook of Combinatorial Designs by Chapman & Hall/CRC.
- Cryptography: The symmetry and structure of magic squares are useful in creating encryption keys and secure communication algorithms.
- Computer Science: Algorithms for generating magic squares support random number generation, data shuffling, and optimization problems.
- Art & Architecture: Magic squares inspire balanced, symmetrical patterns in visual and spatial design.
- Game Theory: Games like Sudoku directly descend from magic square logic, aiding in cognitive development and logic training.
- Education: Used to teach pattern recognition, logic, and arithmetic in engaging, puzzle-like formats.
- Statistics & Experimental Design: Magic square principles help in block design and factorial experiment layouts.
Eastern vs. Western Mathematics: A Reflection
Western mathematical history is often seen as dominating the global narrative, primarily due to its emphasis on abstract theory and formal proof. Eastern traditions, including those in Korea and China, have often taken a more practical and intuitive approach, focusing on problem-solving and empirical applications.
Choi Seok-jeong’s work reveals a different possibility: What if Eastern scholars had also emphasized theoretical abstraction and systemic documentation? Would the East have matched the West in academic mathematics?
His legacy demonstrates that the intellectual capacity certainly existed. It suggests that the East’s relative absence from modern mathematical history may have stemmed not from a lack of genius, but from differing educational philosophies, historical circumstances, and cultural priorities.
Conclusion
Choi Seok-jeong stands as a symbol of Korea’s hidden mathematical brilliance, and a reminder that history often overlooks genius born outside the dominant narrative.
By bringing attention to his world-first 9×9 orthogonal Latin magic square and his pioneering spirit, we recognize a remarkable figure whose work remains relevant across mathematics, computer science, education, art, and beyond.
Let this be a call to scholars, educators, and historians worldwide: Look East, and rediscover the forgotten roots of global science.
Choi Seok-jeong (1646–1715) was a prominent scholar, politician, and mathematician during Korea’s Joseon Dynasty. Renowned for his extensive work in mathematics, particularly in the study of magic squares, he made significant contributions that predated similar discoveries in the West.
Legacy and Recognition
Choi Seok-jeong’s advancements in combinatorial design have been acknowledged in modern mathematical literature. For instance, the Handbook of Combinatorial Designs references his work, noting the historical significance of his 9×9 orthogonal Latin square.
His innovative approaches to magic squares and combinatorial mathematics not only enriched Korean scholarly traditions but also contributed to the global mathematical community, underscoring the universality of mathematical inquiry.
Discover Korea – Related Articles
- The Honil Gangni Yeokdae Gukdo Map: A Symbol of Joseon’s Innovation and Precision
- The 80,000 Woodblocks That Defied Time, War, and Nature
- The Pinnacle of Joseon Scientific Technology
- The Shinkijeon: Korea’s 15th-Century Rocket That Shocked the World
- Redefining the Sky of Joseon – The Scientific Brilliance of Chiljeongsan Naeoe-pyeon
- The Turtle Ship: The World’s First Ironclad Warship and Korea’s Maritime Legacy
- Hallyu: The Global Wave Rooted in Korea’s Ancient Cultural Heritage
- Dolmens of Korea – Ancient Stones, Universal Heritagenergy
- Bigyeokjincheonroe – A Timed Bomb from 16th Century Korea
- Choi Seok-jeong and the World’s First 9×9 Orthogonal Latin Magic Square
- Artificial Intelligence Utilization: Global Insights, Emerging Risks, and a Blueprint for Hardware-Level Safety


