조선의 위대한 수학자 최석정과 마방진 이야기
고차원 마방진 연구로 세계 수학사에 이름을 남긴 조선 후기 수학자의 업적
최석정(崔錫鼎)은 누구인가?

최석정(1646~1715)은 조선 후기의 대표적인 수학자, 정치가, 철학자로, 숙종 시기 학문계를 이끌었던 대학자입니다. 그는 서인 출신이었지만 역모 날조 사건에 반대하며 소론으로 전향했고, 학문과 정치 양쪽에서 큰 발자취를 남겼습니다.
특히 수학, 천문학, 역학 분야에서 뛰어난 업적을 남겨 조선 학문을 세계 수준으로 끌어올렸습니다. 최석정은 실용적 학문을 중시하는 실학적 태도를 견지하며, 실증적이고 체계적인 연구를 진행했습니다.
그가 연구한 9차 직교 라틴 방진은 레온하르트 오일러가 1740년대에 발표한 라틴 방진 연구보다 훨씬 앞선 것으로, 세계 수학사에서 중요한 발견으로 평가됩니다.
마방진이란 무엇인가?
마방진(魔方陣)은 정사각형 배열에서 숫자를 배치해 각 행, 열, 대각선의 합이 동일하도록 만든 배열입니다.
예를 들어 3×3 마방진에서는 모든 행, 열, 대각선의 합이 “15”로 동일하게 맞춰집니다.
마방진은 퍼즐, 주술적 의미, 기하학적 흥미 등 동서양에서 다양한 목적으로 활용되어 왔습니다. 조선에서도 중국 수학서 《구장산술》을 통해 알려졌으며, 최석정은 이를 바탕으로 고차원 마방진 연구에 도전했습니다.
최석정의 마방진 연구
최초의 고차원 마방진
최석정은 기존 2차원 마방진을 넘어 3차원 이상의 고차원 마방진을 체계적으로 연구했습니다. 단순히 숫자를 배열하는 것이 아니라 수학적 규칙과 알고리즘을 적용하여 마방진의 생성 원리를 명확히 밝혔습니다.
《구수략(九數略)》
《구수략》 이미지 위치
최석정의 연구 결과는 수학서 《구수략》에 기록되어 있으며, 조선 시대 수학의 정수를 담은 귀중한 자료로 평가됩니다.
이 책에는 마방진의 이론과 새로운 방진 구조, 알고리즘이 포함되어 있습니다. 특히 그가 만든 9차 직교 라틴 방진은 중국 수학서에는 없는 독창적 연구 결과로, 정교하고 체계적인 방법으로 구성되었습니다.

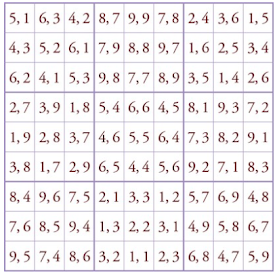
세계 최초의 9차 직교 라틴 마방진
- 9개의 3×3 방진을 조합한 9×9 방진
- 전체 셀의 행, 열, 대각선 합이 같음
- 각 3×3 서브 방진도 합이 동일
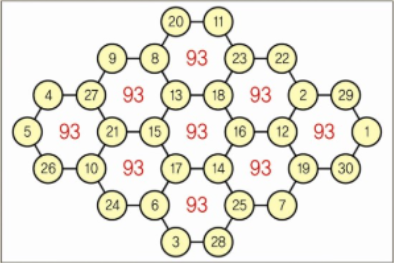
지수귀문도 방진
- 6각 셀 합이 모두 93인 독특한 방진


최석정 마방진 연구의 의의
- 세계 최초 고차 방진 연구
- 3차원 이상 마방진을 체계적으로 연구하고 기록한 최초 사례
- 수학적 체계화
- 놀이 수준에 머물렀던 마방진을 엄격한 수학적 연구 대상으로 승격
- 조선 수학의 위상 강화
- 조선 수학이 동아시아뿐만 아니라 세계 수학 발전에 기여할 수 있음을 보여줌
현대적 평가와 활용
수학과 컴퓨터 과학
- 조합론(Combinatorics), 알고리즘 개발, 난수 생성 등에 영감 제공
- 《Handbook of Combinatorial Designs (2nd Edition, 2007)》에서도 최석정 연구 소개
암호학(Cryptography)
- 대칭성, 균형, 규칙성을 활용한 보안 알고리즘 설계 가능
디자인과 예술
- 대칭성과 규칙성을 활용한 건축, 회화, 장식물 설계
- 미학적 요소와 상징적 의미 표현
퍼즐, 게임, 교육
- **스도쿠(Sudoku)**와 같은 퍼즐에 원리 적용
- 패턴 인식, 문제 해결 능력, 논리적 사고 훈련 도구
공학, 물리학, 통계학
- 구조 설계, 최적화 문제, 블록 디자인(block design) 이론 등에 응용 가능
심리학
- 패턴 인식과 문제 해결 능력 평가, 두뇌 활동 자극
마무리
이번 글에서는 최석정과 마방진에 대해 살펴보았습니다.
많은 사람들이 동양 수학은 서양 수학에 뒤처졌다고 생각하지만, 이는 문화적 접근 방식과 역사적 배경의 차이에서 비롯된 결과입니다.
- 동양 수학: 실용적, 직관적 문제 해결 중심
- 서양 수학: 이론적, 순수 학문적 탐구 중심
최석정의 연구를 보면, 만약 조선이 순수 학문 중심의 수학 문화 속에 있었다면, 서양 수학에 뒤처지지 않았을 가능성도 있습니다.
결국, 동양 수학이 상대적으로 세계사에서 차지하는 비중이 작은 이유와 그 결과를 이해할 수 있는 좋은 사례가 됩니다.


